AI(Artificial Intelligence)
- 인간의 지능을 인공적으로 구현한 것
머신러닝
학습 종류
지도학습
- 정답이 있는 데이터를 활용해 학습
- 정답 라벨이 없는 데이테로 학습
- 비슷한 특징 → 군집화 → 결과 예측
- 데이터 규정 X
- 정답 X
- 한 행동에 보상을 받으며 학습 → 보상 최대화
지도학습의 종류
회귀(regression)
- 값을 예측하는 방식
- 대표적으로, 선형 회귀(Linear Regression)가 있음.
분류(Classification)
- True, False 판별
- 로지스틱 회귀(Logistic Regression)가 대표적.
선형 회귀(Linear Regression)
단순 선형 회귀
y=wx+b(w=weight,b=biased)y = wx + b(w = weight, b = biased)
다중 선형 회귀
y=w1∗x1+w2∗x2+b(w1,w2=weight,b=biased)y = w1 * x1 + w2 * x2 + b(w1, w2 = weight, b = biased)
오차 계산법
- 평균 제곱 오차(MSE, Mean Squared Error)
- 차이를 제곱하여 평균 낸 값
- MSE=1nΣ(y^−y)2(y^=PredictedValue)MSE = {1 \over n}\Sigma(\hat{y} - y)^2 (\hat{y} = Predicted Value)
- 평균 절대값 오차(MAE, Mean Absolute Error)
- 차이의 절대값을 평균낸 값
- MAE=1nΣ∣y^−y∣(y^=PredictedValue)MAE = {1 \over n}\Sigma|\hat{y} - y| (\hat{y} = Predicted Value)
MSEMSE 그래프의 모양을 나타내면 다음과 같다.

오차가 가장 작은 지점의 기울기는 0, 따라서 미분값이 0인 지점의 W, b 의 값을 구하면 된다.
구하는 과정은 다음과 같다.
w 값을 구하는 과정
같은 방법으로 b의 값을 구하면,
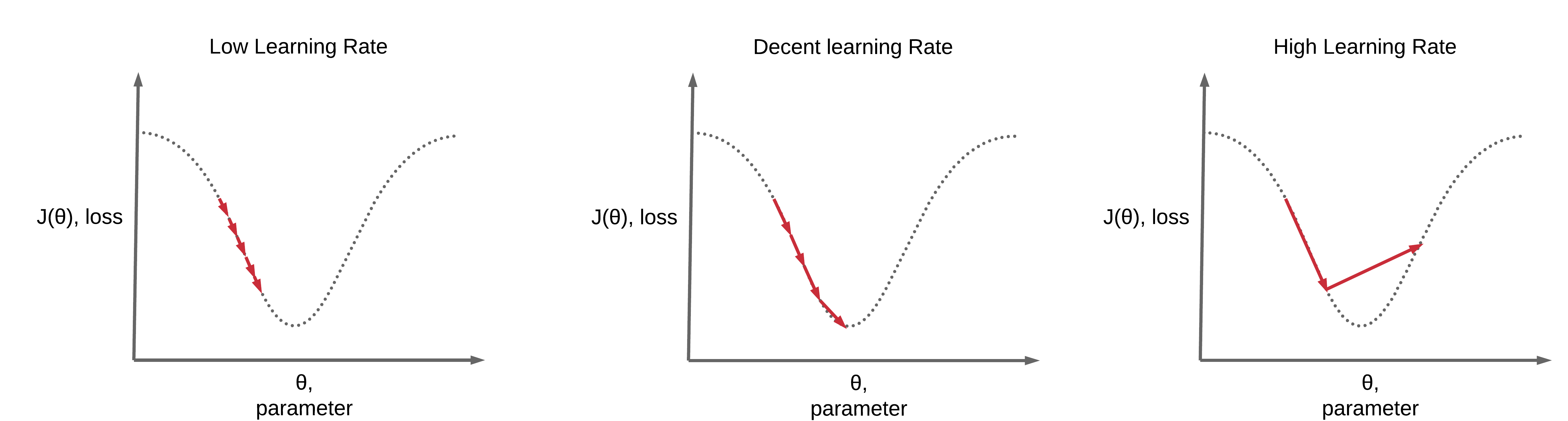
학습률(Learning Rate)
- Learning Rate 가 너무 크면, 발산할 위험이 있고, 너무 작으면 제대로 학습되지 않을 수 있음.
- 적절한 조율 필요
단순 선형 회귀 경사하강법 code
import numpy as np import matplotlib.pyplot as plt x_train = np.random.rand(100) y_train = 1000 * x_train + 500 def plot_prediction(pred): plt.figure(figsize=(10, 10)) plt.scatter(x_train, y_train) plt.scatter(x_train, pred) plt.draw() plt.pause(0.5) plt.close() w = np.random.uniform(-1, 1) # 초기값 설정(기울기) b = np.random.uniform(-1, 1) # 초기값 설정(y절편) learning_rate = 0.7 for epoch in range(1000): y_pred = w * x_train + b error = np.abs(y_pred - y_train).mean() if error < 0.001: break w_grad = learning_rate * ((y_pred - y_train)*x_train).mean() b_grad = learning_rate * (y_pred - y_train).mean() w -= w_grad b -= b_grad if epoch % 10 == 0: print("[" + str(w) + "] [" + str(b) + "] [" + str(error) + "]") y_pred = w * x_train + b plot_prediction(y_pred) print("[" + str(w) + "] [" + str(b) + "] [" + str(error) + "]") #참고자료: https://s.sheenji.com/VCg2gL
다중 선형 회귀 경사하강법 code
import numpy as np import matplotlib.pyplot as plt x1_train = np.random.rand(100) x2_train = np.random.rand(100) y_train = 1000 * x1_train + 100 * x2_train + 500 w1 = np.random.uniform(-1, 1) # 초기값 설정(기울기 1) w2 = np.random.uniform(-1, 1) # 초기값 설정(기울기 2) b = np.random.uniform(-1, 1) # 초기값 설정(y절편) learning_rate = 0.7 for epoch in range(1000): y_pred = w1 * x1_train + w2 * x2_train + b error = np.abs(y_pred - y_train).mean() if error < 0.001: break w1_grad = learning_rate * ((y_pred - y_train)*x1_train).mean() w2_grad = learning_rate * ((y_pred - y_train)*x2_train).mean() b_grad = learning_rate * (y_pred - y_train).mean() w1 -= w1_grad w2 -= w2_grad b -= b_grad if epoch % 10 == 0: print("[" + str(w1) + "] [" + str(w2) + "] [" + str(b) + "] [" + str(error) + "]") print("[" + str(w1) + "] [" + str(w2) + "] [" + str(b) + "] [" + str(error) + "]") #참고자료: https://s.sheenji.com/VCg2gL